Samarthya

Life can change any moment, and I am ready for it.

About Me

Mastering TF-IDF: A Gamified Journey!

Saurabh Sharma 3 weeks ago

Understanding how computers “read” and understand text is a fascinating field. One of the most fundamental techniques for identifying important keywords in a document, relative to a collection of documents, is TF-IDF (Term Frequency-Inverse Document Frequency).

I recently embarked on a gamified learning challenge to demystify TF-IDF, breaking it down into its core components. This post summarizes my adventure!

The Core Idea: Why TF-IDF Matters

Imagine you have a huge library of books. If you want to find out what a specific book is really about, just looking at words that appear frequently isn’t enough. “The” or “is” might appear often, but they tell you nothing unique. TF-IDF helps us find words that are:

  1. Frequent within a specific document (TF)
  2. Rare across the entire collection of documents (IDF)

When a word meets both criteria, it’s likely a powerful keyword that defines that document’s content.

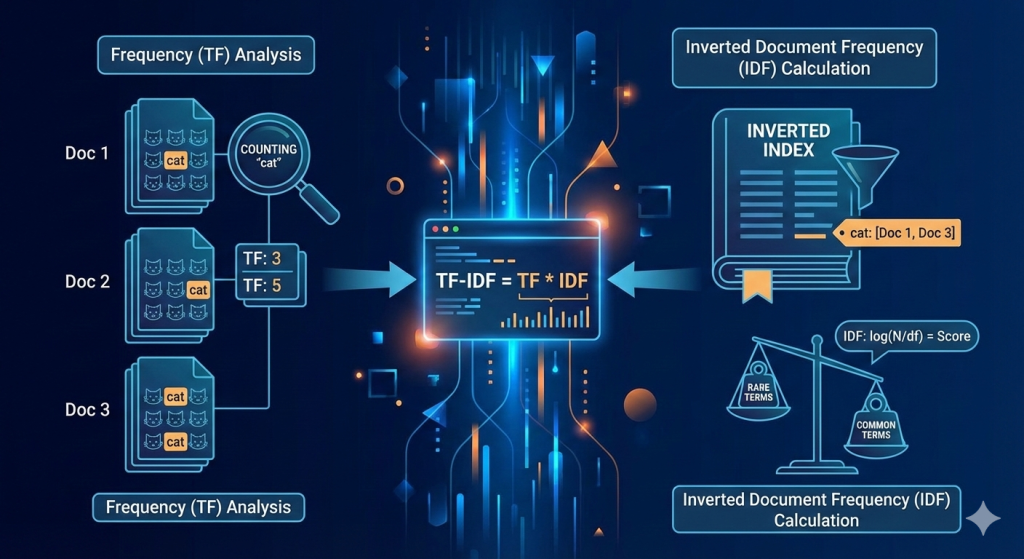
Level 1: Term Frequency (TF) – How Often Does a Word Appear?

Term Frequency is the simplest part. It’s just a count of how often a word (term) appears in a document, normalized by the total number of words in that document.

Formula:

TF(t,d)=Number of times term t appears in document dTotal number of words in document d\text{TF}(t, d) = \frac{\text{Number of times term } t \text{ appears in document } d}{\text{Total number of words in document } d}

Example:

Let’s say we have Document A:

“The cat sat on the mat. The cat is black.”

  • Total words in Document A: 10
  • Term ‘cat’ appears: 2 times

Calculation:

TF(cat,A)=210=𝟎.𝟐\text{TF}(\text{cat}, \text{A}) = \frac{2}{10} = \mathbf{0.2}

A higher TF means the word is more important to that specific document.

Level 2: Inverse Document Frequency (IDF) – How Unique is a Word Across Documents?

Here’s where TF-IDF gets clever. IDF helps us ignore common words (like “the”) that appear in almost every document. It assigns a higher score to words that are rare across our entire collection of documents (our “corpus”).

Formula (General form):

IDF(t,D)=log⁡(Total number of documents NNumber of documents containing term t)\text{IDF}(t, D) = \log \left( \frac{\text{Total number of documents } N}{\text{Number of documents containing term } t} \right)

Our Corpus (4 Documents):

  • D1: “The cat sat on the mat.”
  • D2: “The dog chased the frisbee.”
  • D3: “I like my cat.”
  • D4: “My neighbor’s cat is cute.”

Calculations (using natural logarithm):

  • For ‘cat’: Appears in D1, D3, D4 (3 documents out of 4)
IDF(cat,D)=ln⁡(4/3)≈𝟎.𝟐𝟖𝟕\text{IDF}(\text{cat}, D) = \ln(4/3) \approx \mathbf{0.287}
  • For ‘frisbee’: Appears in D2 (1 document out of 4)
IDF(frisbee,D)=ln⁡(4/1)≈𝟏.𝟑𝟖𝟔\text{IDF}(\text{frisbee}, D) = \ln(4/1) \approx \mathbf{1.386}

Notice: ‘frisbee’ (rare) gets a much higher IDF than ‘cat’ (relatively common).

Level 3: The TF-IDF Score – Combining Frequency and Uniqueness

The final TF-IDF score is simply the product of TF and IDF. This score highlights words that are both frequent in a document and unique across the corpus.

Formula:

TF-IDF(t,d,D)=TF(t,d)×IDF(t,D)\text{TF-IDF}(t, d, D) = \text{TF}(t, d) \times \text{IDF}(t, D)

Putting it Together:

  • TF for ‘cat’ in Document A: 0.2
  • IDF for ‘cat’ in Corpus: 0.287
TF-IDF(cat,A,D)=0.2×0.287≈𝟎.𝟎𝟓𝟕𝟒\text{TF-IDF}(\text{cat}, \text{A}, D) = 0.2 \times 0.287 \approx \mathbf{0.0574}
  • Hypothetical TF for ‘frisbee’ in a document: 0.1 (e.g., if ‘frisbee’ appeared once in a 10-word document)
  • IDF for ‘frisbee’ in Corpus: 1.386
TF-IDF(frisbee,hypothetical doc,D)=0.1×1.386≈𝟎.𝟏𝟑𝟖𝟔\text{TF-IDF}(\text{frisbee}, \text{hypothetical doc}, D) = 0.1 \times 1.386 \approx \mathbf{0.1386}

Result: Even with a lower term frequency, ‘frisbee’ has a higher overall TF-IDF score because its uniqueness (high IDF) boosts its importance.

This is the magic of TF-IDF!